Φράκταλ

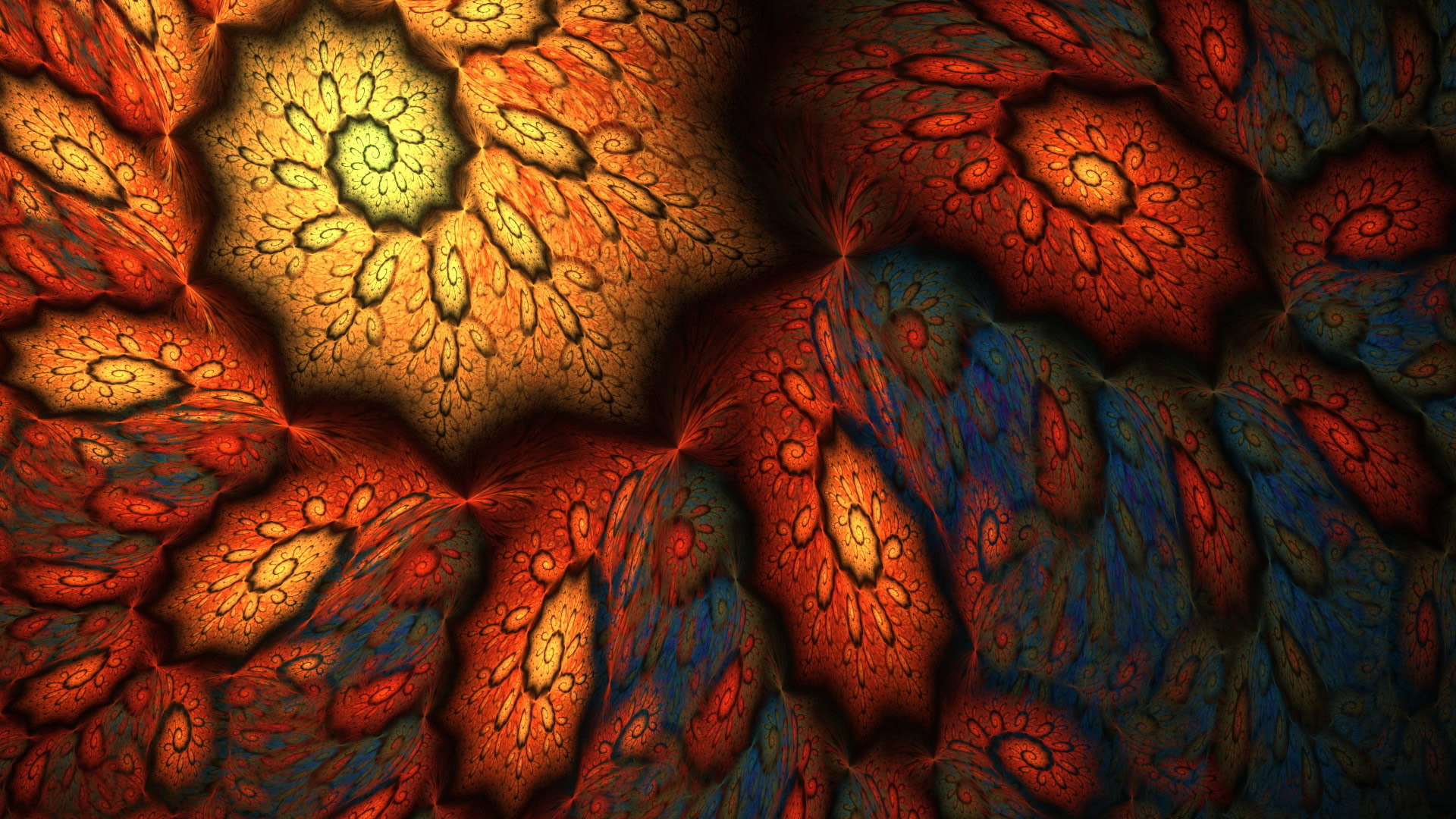
Η ακανόνιστη γεωμετρία των φράκταλ.

Η γεωμετρία των Φράκταλ

Στην εποχή της κλασικής επιστήμης, εξαιτίας της έλλειψης τεχνικής για την αντιμετώπιση μη γραμμικοτήτων, εμφανιζόταν η διαδικασία της γραμμικοποίησης των μη γραμμικών εξισώσεων με την απομάκρυνση όλων των μη γραμμικών όρων της εξίσωσης, καθώς είναι συνήθως ευκολότερο να λυθούν οι γραμμικές εξισώσεις από τις μη γραμμικές. Απεδείχθη όμως ότι στη φύση κυριαρχεί η μη γραμμικότητα. Κατά τη δεκαετία του 1970, μερικοί επιστήμονες στις ΗΠΑ και στην Ευρώπη άρχισαν να προσεγγίζουν την έννοια της αταξίας. Μια δεκαετία αργότερα, το χάος έγινε το σύμβολο ενός  κινήματος, το οποίο αναπτύσσεται αστραπιαία και διαμορφώνει τη σύγχρονη επιστημονική πραγματικότητα. Το χάος έχει δημιουργήσει ειδικές τεχνικές στη χρήση των υπολογιστών και έχει δημιουργήσει τη δική του γλώσσα, με λέξεις όπως Φράκταλ, διακλαδώσεις και περιοδικότητες. Τα τελευταία χρόνια που η επιστήμη άρχισε να το αναζητά, το χάος φαίνεται να υπάρχει παντού.

Φράκταλ ή παράξενοι ελκυστές

Το 1971 ο Βέλγος φυσικός Νταβίντ Ρουέλ και ο Ολλανδός μαθηματικός, Φλόρις Τάκενς έκαναν μια σπουδαία συνεισφορά στον κόσμο της φυσικής με μια εικόνα μέσα στο άρθρο που δημοσίευσαν, “On the Nature of Turbulence”, που οι συγγραφείς ονόμασαν παράξενο ελκυστή. Οι παράξενοι ελκυστές χαρακτηρίζονται από δύο ιδιότητες: την ευστάθεια και τη μη περιοδικότητα. Μακροπρόθεσμα όμως, οι μόνες δυνατές συμπεριφορές είναι οι ίδιοι οι ελκυστές, καθώς η κίνηση τείνει να επιστρέφει σ’ αυτούς. Επιπλέον, οι παράξενοι ελκυστές είναι μη περιοδικοί, δεν επαναλαμβάνεται ποτέ.

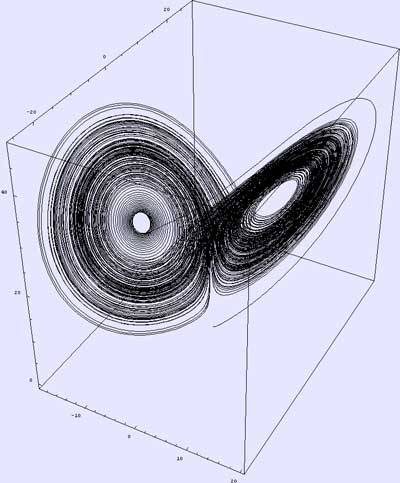
Από γεωμετρική άποψη, η τροχιά κινούμενη σε έναν πεπερασμένο χώρο δεν επαναλαμβάνει ποτέ τον εαυτό της και δεν τέμνει ποτέ τον εαυτό της (από τη στιγμή που ένα σύστημα επιστρέφει σε μια κατάσταση στην οποία είχε βρεθεί πριν, πρέπει πάντα να ακολουθεί την ίδια πορεία). Οι γραμμές της τροχιάς δεν διασταυρώνονται ποτέ, γιατί έχουν απεριόριστο βάθος. Είναι δηλαδή φράκταλ (μορφόκλασμα ή μορφοκλασματικό σύνολο).

Η Ευκλείδεια γεωμετρία υπήρξε πάρα πολύ χρήσιμη και επηρέασε την άποψη που έχουμε για τον κόσμο για περισσότερο από δύο χιλιετίες.  Αλλά στην κατανόηση της πολυπλοκότητας η γεωμετρία αυτή αποδεικνύεται ένα λαθεμένο είδος αφαίρεσης. Η ευκλείδεια γεωμετρία χωλαίνει όταν έρχεται να περιγράψει οτιδήποτε είναι ακανόνιστο, ασυνεχές ή τραχύ. Τα περισσότερα πράγματα στη φύση δεν χαρακτηρίζονται από κανονικότητα. Ο Μπενουά Μάντελμπροτ εισάγει στο σημείο αυτό μια καινούρια έννοια, που μας βοηθά να περιγράψουμε το ακανόνιστο: την έννοια της «διάστασης». Σύμφωνα με την ευκλείδεια γεωμετρία ο χώρος έχει τρεις διαστάσεις, το επίπεδο δύο, η γραμμή μία και το σημείο καμία.

Ο Μάντελμπροτ ισχυρίστηκε ωστόσο ότι τα αντικείμενα αλλά και τα σημεία παρουσιάζουν διαφορετικές διαστάσεις ανάλογα από την απόσταση που τα εξετάζουμε, προχωρώντας, πέρα από τις γνωστές τρεις διαστάσεις, στις κλασματικές διαστάσεις, δηλαδή στις διαστάσεις εκείνες που δεν εκφράζονται με ακέραιους αριθμούς, αλλά με κλάσματα. Έτσι την απουσία κανονικότητας τη μετράμε με την κλασματική διάσταση και βλέπουμε την ικανότητα του ακανόνιστου αντικειμένου να πιάνει όσο το δυνατόν περισσότερο χώρο. Ο Μαλντεμπροντ ονόμασε αυτά τα αντικείμενα ακανόνιστου σχήματος fractal από την λατινική λέξη “fractus”, που σημαίνει “ακανόνιστο/σπασμένο”.

Για να μας δώσει να καταλάβουμε την έννοια της γεωμετρίας των φράκταλ, ο Μαλντεμπροντ έθεσε το εξής ερώτημα σε ένα άρθρο του: “Τι μήκος έχει η ακτή της Βρετανίας?”. Η απάντηση του ήταν ότι το μήκος εξαρτάται από την απόσταση που θα μετρήσουμε. Το μήκος της ακτής για παράδειγμα διαφέρει άμα τη κοιτάς από ένα αεροπλάνο, μιας και θα δεις ένα γενικό και ακανόνιστο σχήμα, χωρίς κολπίσκους και παραλίες. Το μήκος που θα μετρήσεις θα είναι σίγουρα μικρότερο του πραγματικού.

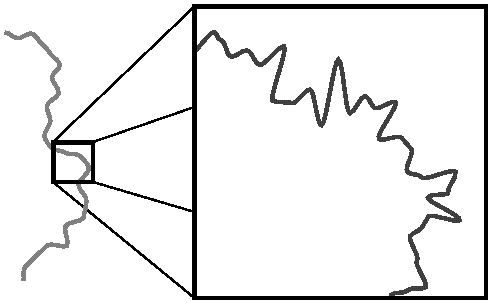
Αν τώρα όμως τη διατρέξουμε με το αυτοκίνητο θα παρατήρησουμε πολύ περισσότερες λεπτομέρειες και το μήκος που θα μετρήσουμε θα είναι πολύ πιο κοντά στο πραγματικό. Ωστόσο και πάλι κάποιες εσοχές και κάποιες πολύ μικρές “δαντελωτές” λεπτομέρειες θα μας διαφύγουν. Ένα μυρμήγκι που διασχίζει την ακτή χιλιοστό προς χιλιοστό θα δει τις πολύ πολύ ανεπαίσθητες λεπτομέρειες τις ακτής, και θα μετρήσει και τον παραμικρό κόκκο άμμου. Ακόμα όμως και το μυρμήγκι θα χάσει μερικές απειροελάχιστες λεπτομέρειες.

Άρα το μήκος των ακανόνιστων σχημάτων δε μπορούμε να το υπολογίσουμε?

Η απάντηση είναι πως στα φράκταλ υπάρχει τελικά κανονικότητα στον ακανόνιστο χαρακτήρα τους. Ο βαθμός της μη κανονικότητας παραμένει σταθερός σε διαφορετικές κλίμακες. Έχουν δηλαδή “αυτο-ομοιότητα”. Η όψη τους παραμένει ίδια όσο και να τα μεγεθύνουμε. Παρουσιάζουν δηλαδή ένα μοτίβο απείρως επαναλαμβανόμενο στο εσωτερικό ενός ίδιου μοτίβου που βρίσκεται στο εσωτερικό ενός ίδιου μοτίβου κλπ.

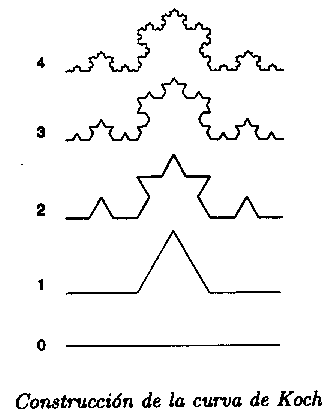
Ο Μάλντεμπροντ στην πορεία των ερευνών του ήρθε αντιμέτωπος με πολλά πολύπλοκα σχήματα που περιγράφουν την έννοια των φράκταλ, όπως η Καμπύλη του Κοχ, οι καμπύλες του Πεάνο, τα κόσκινα Σιερπίνσκι. Όλα αυτά τα πολύπλοκα σχήματα χαρακτηρίζονται από την άπειρη επανάληψη της μη κανονικότητας τους μέσα στον εαυτό τους, με ένα βαθμό σταθερό. Αυτά τα σχήματα καταλάμβαναν πολύ περισσότερο το χώρο από ό,τι η κλασσική ευκλείδεια γεωμετρία. Για παράδειγμα η Καμπύλη του Κοχ έχει ένα άπειρο μήκος το οποίο συνωστίζεται σε μια πεπερασμένη επιφάνεια. Έτσι δημιουργεί κάτι περισσότερο από γραμμή αλλά κάτι λιγότερο από επίπεδο. Είναι πάνω από μια διάσταση, αλλά είναι λιγότερο από δύο διαστάσεις. Ο Μάλντεμπροντ βρήκε ότι η κλασματική διάσταση στην οποία ανήκει η καμπύλη του Κοχ είναι 1,2618.

Τα φράκταλ μας αφορούν άμεσα, γιατί παρατηρούμε ότι η φύση έχει μεγάλη συμπάθεια στα φράκταλ και λειτουργεί με τους “κανόνες” τους. Τα δέντρα, τα φύλλα, τα αιμοφόρα αγγεία, οι ακτές των θαλασσών κλπ. Όλα τα στοιχεία από το μικρόκοσμο μέχρι και τον μακρόκοσμο ακολουθούν τον σχηματισμό του ακανόνιστου. Πρόκειται για σχήματα που έχουν προέλθει από δυναμικές διαδικασίες και μέσα τους συνυπάρχουν θαυμαστοί συνδυασμοί τάξης και αταξίας.